Normalized Dicounted Cumulative Gain(NDCG)
The premise of DCG is that highly relevant documents appearing lower in a search result list should be penalized as the graded relevance value is reduced logarithmically proportional to the position of the result. The discounted CG accumulated at a particular rank position p is defined as:
When given a ground truth ranking, we could have a ideal DCG(IDCG). For a query, the normalized discounted cumulative gain, or NDCG, is computed as:
In our case, the new Recomen system given out a new rank. rel is the stars one user rated on one restaurant. The ground truth ranking is a ranking sort by the stars. For one user, we only test the ranking on all the restaurants he/she has ever rated and take NDCG@last.
Considering of there is some users who have only rated several restaurants(for example 3), or they only rate 5 stars, their NDCG@last is not meaningful in evaluation. So we set an threshold n, if the user-rated restaurants are more than n restaurants and the user's rating are more than 2 kinds, we will let this user in our evaluation set.
Models Evaluation
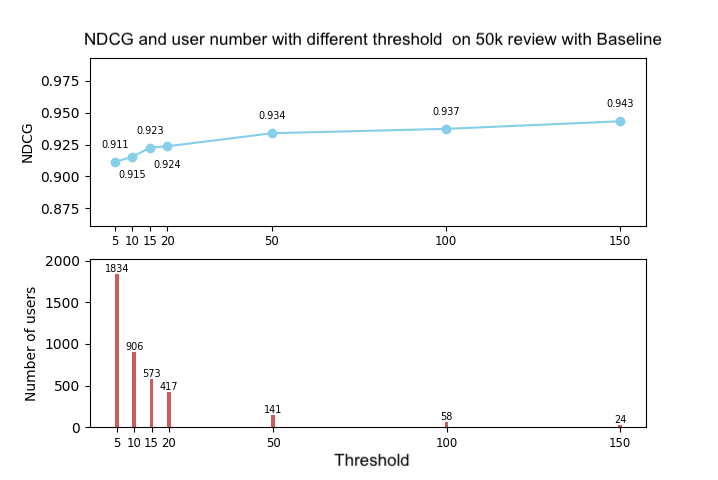
Baseline
For every user in our evaluation set, we calulate the NDCG@last witin a randomly shuffled ranks of all the restaurants he/she has rated. The result shows if we do nothing, what NDCG@last would we get.
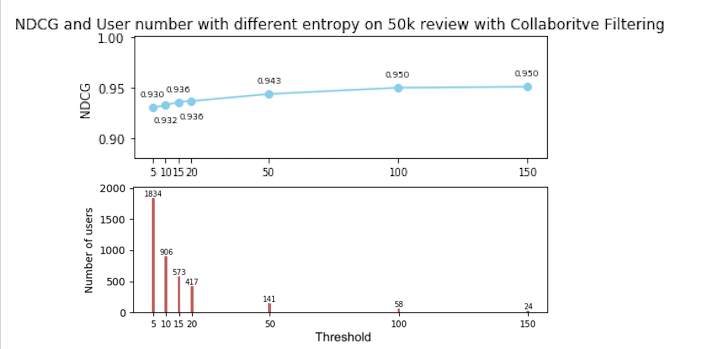
Collaborative Filtering
The users are selected as in the baseline. This time we test the ranks sorted by the predicting scores given by collaborative filtering. The result is showed below. Also, the speed of CF is very slow, to run the 50k database, our program runs about 450s.
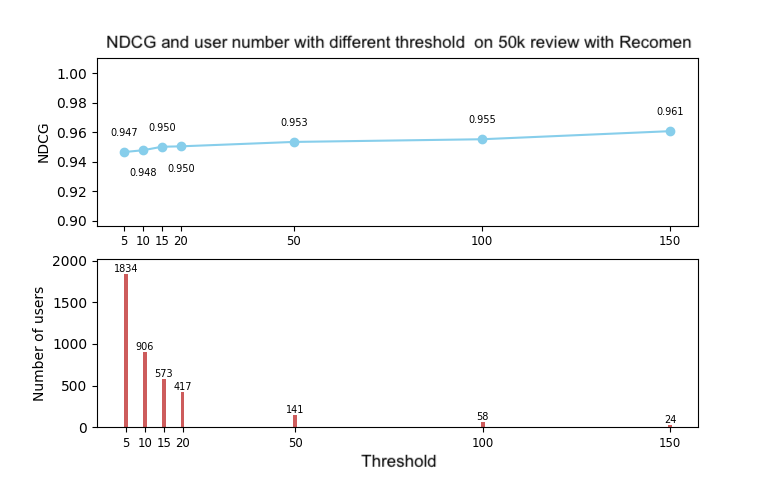
Recomen
The users are selected as before and we test the ranks sorted by the scores we get. The result is showed below. And the speed is far higher than collabrative filtering, to run the 50k database, it use about 7s.
Comparison
| Model | NDCG@last with 20 threshold | Running time (s) |
|---|---|---|
| Baseline | 0.924 | -- |
| Collaborative Filtering | 0.936 | 453.4 |
| Recomen | 0.950 | 7.6 |
Thus, our model has done a good job on recomending new restaurants to a user. Also our model is with good interpretability than a Lantent Factor Model.
LSH Speeding
We also apply LSH on our algorithm to speed up the search. We test it on another computer which runs a lot slowlier than the one we normly use. We run the recomendation algorithm on 20 users to see the total time.
| Model | Running time (s) |
|---|---|
| Recomen without LSH | 541.24 |
| Recomen with LSH | 52.98 |